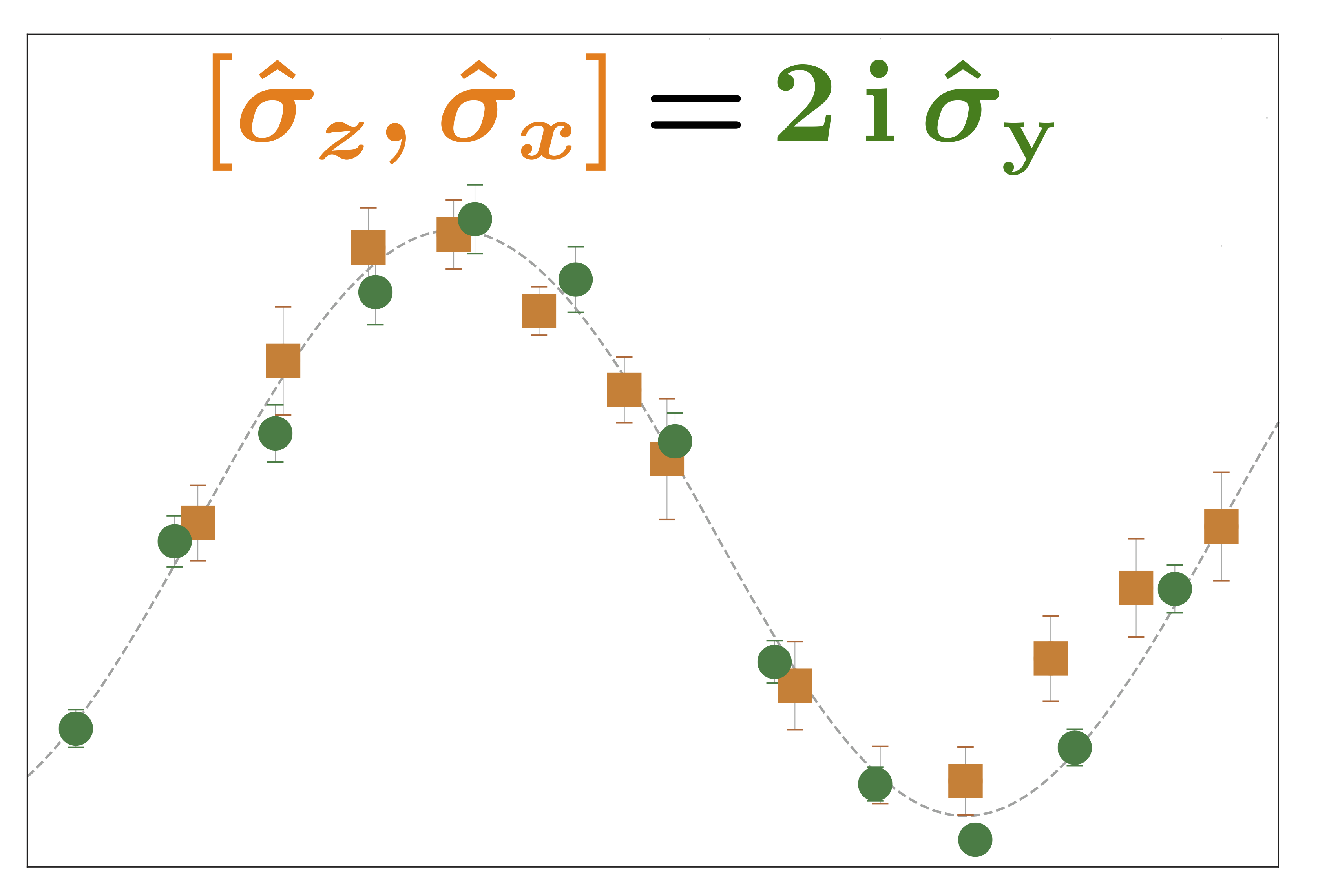
Direct experimental test of commutation relation via imaginary weak value

In our latest work ¹, we tested canonical commutation in an interferometric experiment. The canonical commutation relation is a tenet of quantum theory and Heisenberg’s uncertainty relation is a direct consequence of it. Without loss of generality, consider two non-commuting qubit observables, say and satisfying for all where is a nonzero quanity. Since the product may not be Hermitian in general, the traditional von Neumann quantum measurement scheme cannot be carried but the weak measurement sufficed for our purpose. Non-Hermitian observables may be measured using weak measurements. But our scheme here is direct and fundamentally different, as follows. If and are positive-eigenvalue projectors of and respectively, then by using the definition of projection operators and , one has , where is the weak value of the projector for a post-selected state and pre-selected state and is the probability of successful post-selection. If and , the commutation relation reads . By writing , and where , and are the projectors with positive eigenvalue corresponding to the observables , and , respectively. It follows , where is the weak value of given the pre- and post-selected states and , respectively. Thus, the imaginary part of a single weak value is suited to test the commutation relation.

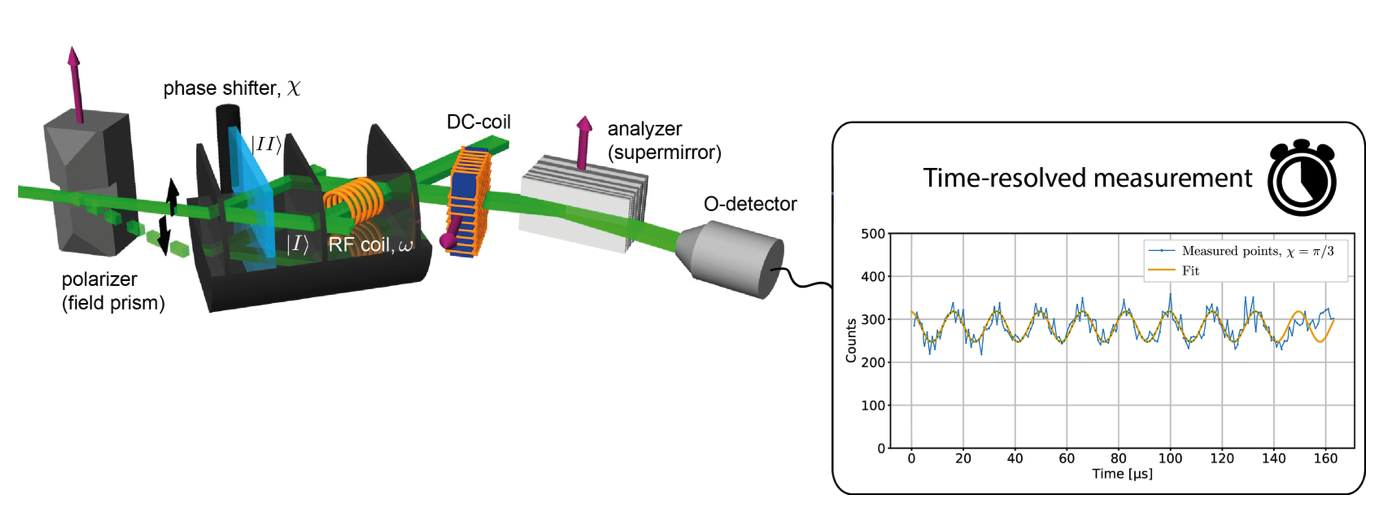
To determine the weak value of the path projector onto path 1, denoted as , an established neutron interferometric setup suited to carry out weak measurements (see here for theoretical backgroud), depicted above, is applied. The system is prepared (pre-selected) in the initial path state  and post-selected in final state . In order to weakly couple the path degree of freedom to the ancilla, which is represented by the coupled spin-energy degree of freedom, a weak spin rotation via an RF coil is induced in path 1. This RF spin manipulation (see here for theory )leads to an energy-shift by the amount in the spin-flipped parts and can be written as a unitary operator:
 where , and are the spin-rotation angle, the frequency of the electromagnetic RF field and an arbitrary phase of this RF field, respectively. The energy-shifted contributions appear due to the off-diagonal terms. The parameter is related to magnetic field strength and for a small value of becomes:
. This results in a time dependent interference pattern of intensity . The weak value for the path projector is a complex number and can therefore be written in the polar form , which is compared to the time dependent interference pattern, expressed in amplitude and phase as , which is depicted below.

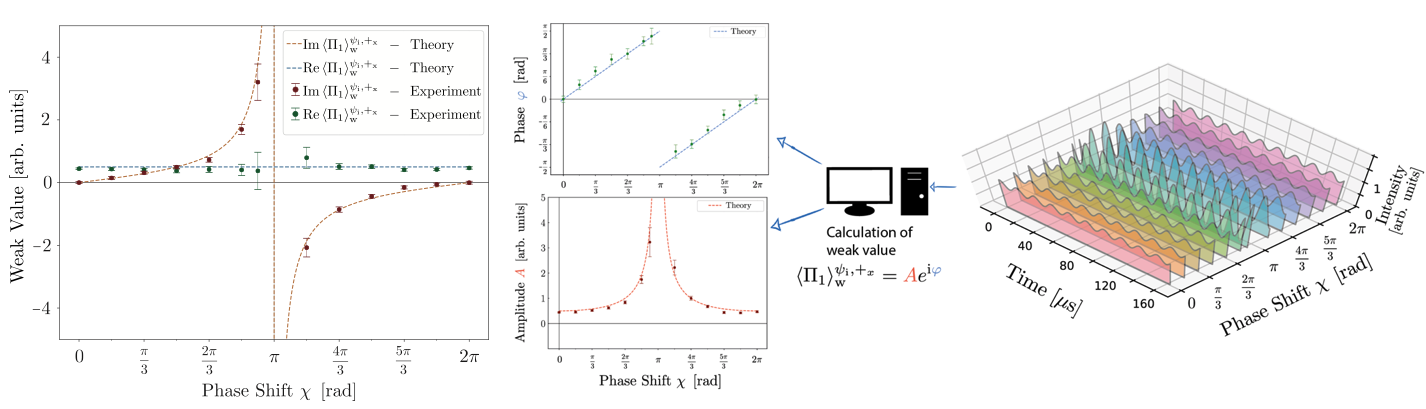
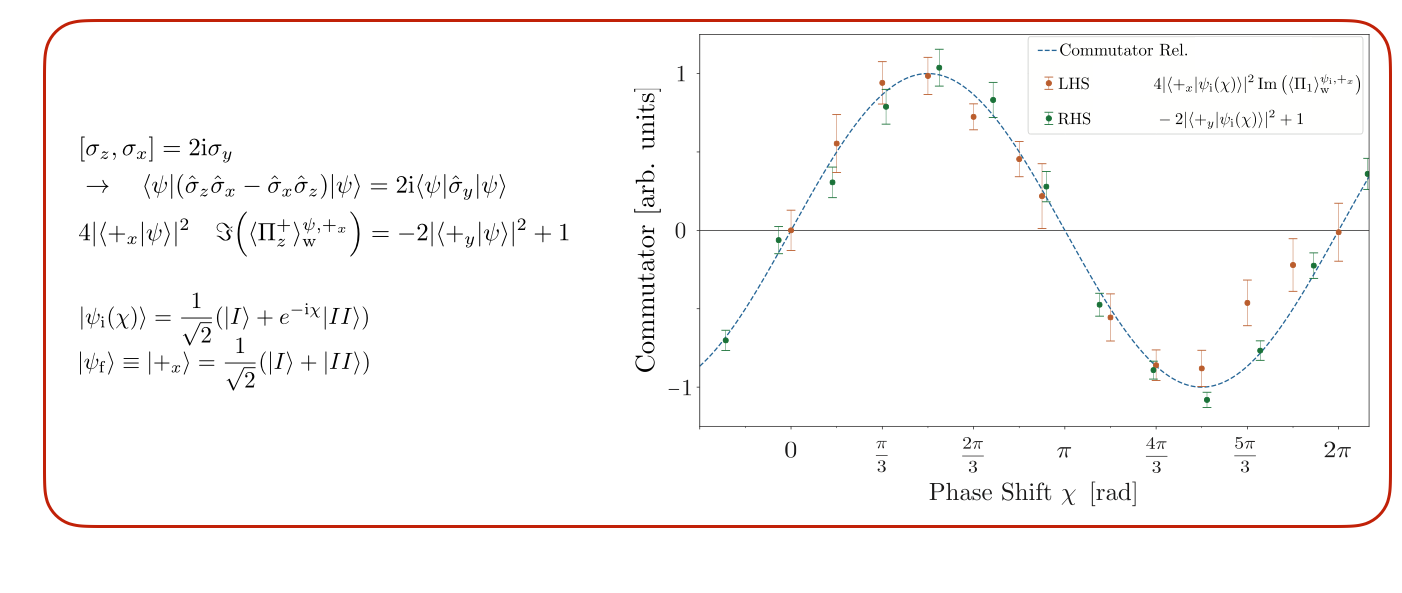
By switching off the RF field, two post-selected probabilities and are measured. Finally, the results of all three measurements, that is , and , are combined, for the direct test of the commutation relation, which can be seen below.

1. R. Wagner, W. Kersten, A. Danner, H. Lemmel, A. K. Pan, and S. Sponar Phys. Rev. Research 3, 023243 (2021). ↩