Test of completeness of quantum root-mean-square errors

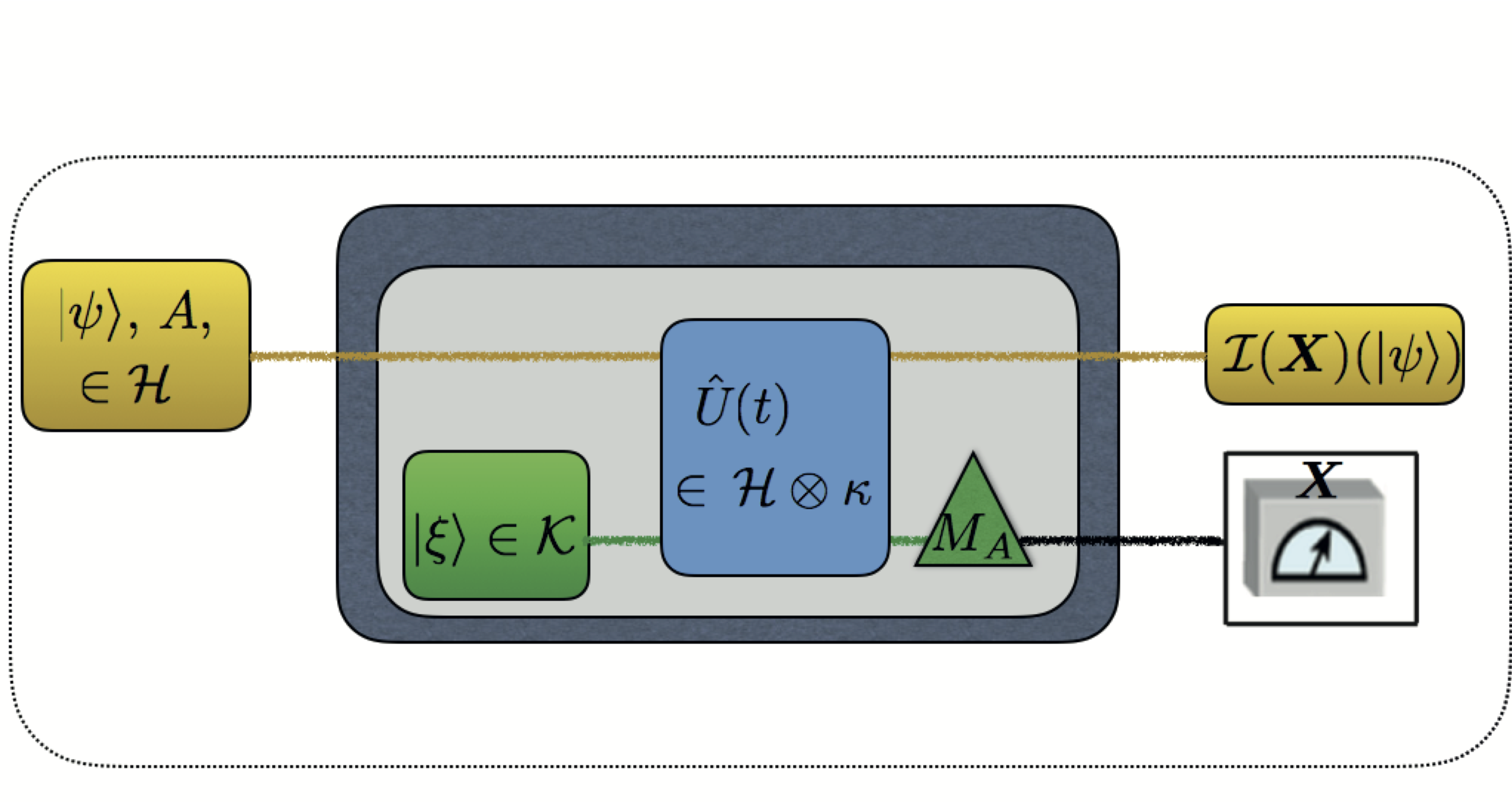
In our latest work ¹ we study the reliability of errors in the quantum measuring process via neutron spin measurements. While in classical mechanics the mean error of a measurement is solely caused by the measuring process (or device), in quantum mechanics the operator-based nature of quantum measurements has to be considered in the error measure as well. One of the major problems in quantum physics has been to generalize the classical root-mean-square error to quantum measurements to obtain an error measure satisfying both soundness (to vanish for any accurate measurements) and completeness (to vanish only for accurate measurements). A noise-operator based error measure has been commonly used for this purpose, but it has turned out incomplete. Recently, Ozawa proposed an improved definition for a noise-operator-based error measure to be both sound and complete. Recently, Ozawa proposed an improved definition for a noise-operator-based error measure to be both sound and complete ².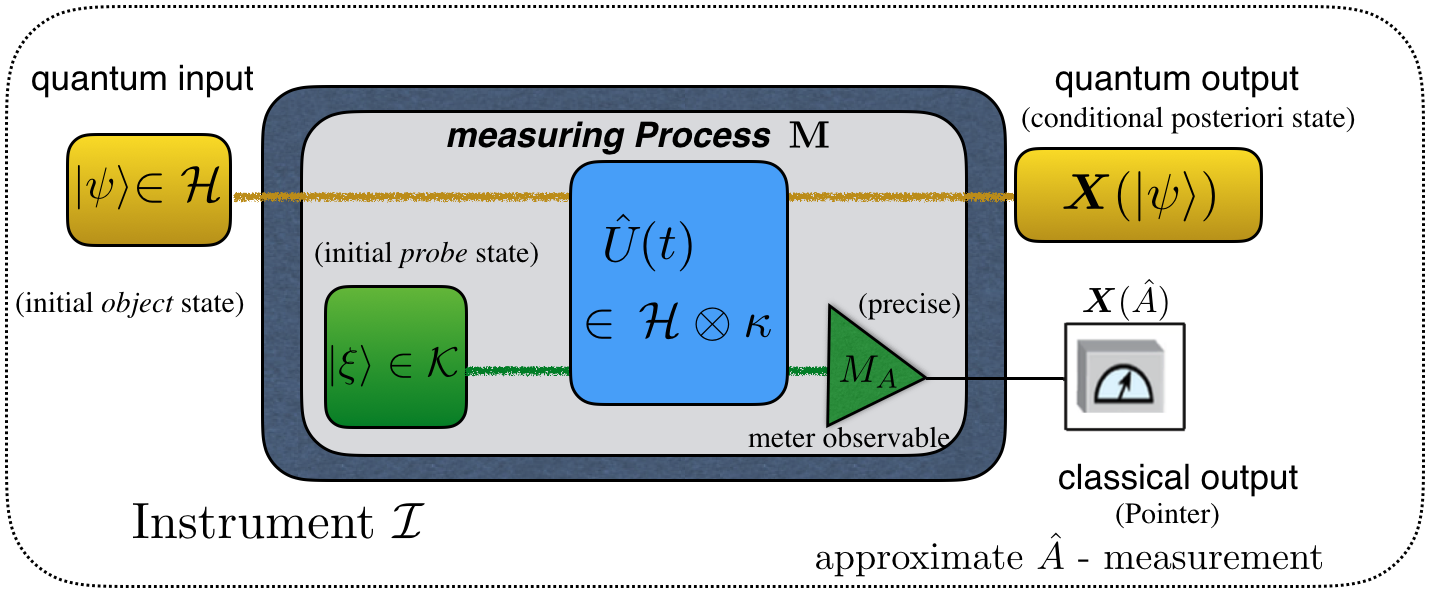 The noise-operator based quantum root-mean-square (q-rms) error of a measuring process , on quantum instrument , is denoted as , where the noise-operator describes how accurately the value of an observable is transferred to the meter observable , during the evolution of the composite system: . Here, is an observable of a system in state of Hilbert space , and is the observable representing the meter of the observer in the probe system (measurement device) in initial state of Hilbert space . Moreover, is the unitary evolution of the composite quantum system . This concept, is usually referred to as indirect measurement model of measuring process and schematically illustrated aside. Furthermore, we have and . The POVM of the measuring process is defined by , where is the spectral projection of for eigenvalues . The moment (mean) operator of the POVM is defined by , and the second moment operator of the POVM is defined by . The measurement is called a sharp or projective measurement of if is projection-valued. In this case, we have and . Otherwise, the measurement is called an unsharp (or generalized) measurement of with . An important property of is that it is determined by (moment operators of) the POVM of in such a way that for general (unsharp), which in the case of sharp (projective) measuresment reduces to .

It is shown by Busch, Lahti, and Werner (BLW) ³ that there exists a measuring process with , whereas does not accurately measure . However, a vanishing error is only expected for an accurate measurement for the completeness of the error measure. Consider a measurement of the observable in a two-level system in the initial state with measuring process described by a POVM with the moment operator given as follows: , , and . We consider the sharp measurement of with the POVM , in this case, one obtains and , so that . However, this particular measurement is not accurate, since and have disjoint spectra: operator has spectral decomposition , 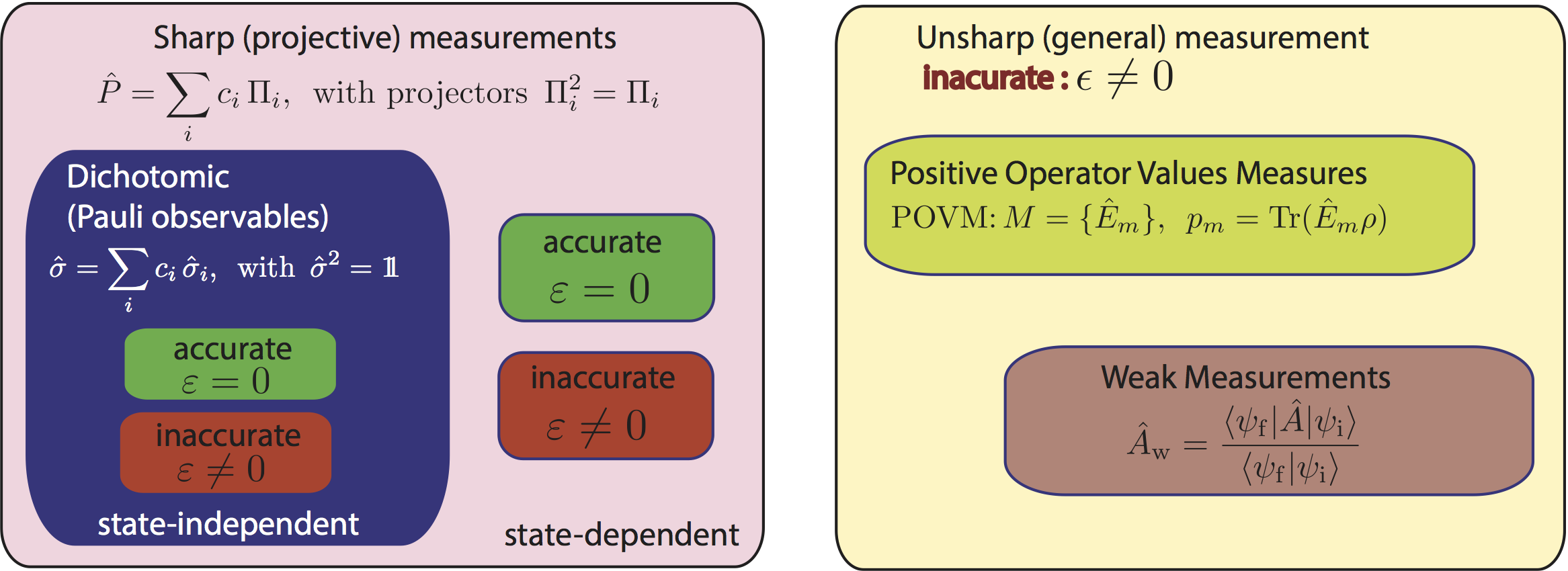with eigenvalues and normalized eigenvectors , while , with eigenvalues and normalized eigenvectors . With , being the projector associated with eigenvalue 2, that is , which finally gives . We can then write to express the inaccuracy of the measurement. Thus, the measurement with the POVM does not accurately measure but , which is problematic – or in other words – the quantum root-mean-square error is incomplete. To remedy the incompleteness of the noise-operator based q-rms error, Ozawa proposed a modification of its definition ² : For any t the quantum root-mean-square (q-rms) error profile for and in is defined as . In order to obtain a numerical error measure the locally uniform q-rms error is given by , resulting in a sound and complete q-rms error . For the given example from above we get and , resolving the problem.

For the actual experiment (setup is depicted above), the time evolution of the initial state , dependent on needs to be analyzed;. The observable can be decomposed as . Hence, the time evolution of the initial state yields , which is simply a rotation about the -axis by an angle (see Bloch sphere). Thus the parametrization has changed from time to an (experimentally adjustable) spinor rotation angle . Applying the well known three-state-method for generalized measurements to obtain the state-dependent q-rms error profile from , where denotes the second moment of , given by . The first term can be symmetrized, applying the operator identity , which gives a sum of experimentally accessible expectation values , where the last term vanishes for projective measurements.

In order to demonstrate the counter example from above, a sharp measurement of is required. The decomposition of into projectors is denoted as , where and with . According to the three-state method the error-profile is obtained by measuring expectation values of , and in state and of in auxiliary states and , which is plotted below for in state (see here for results of the individual expectation vales).

Summing up all five terms finally gives , with locally uniform q-rms error , which is plotted below for 13 values of , together with Bloch sphere of initial state and measurement direction of the projective measurement of M (note that only for Pauli spin matrices  measurements the first two terms of Equation are unity and the error profiles becomes -independent).

In addition, we consider the unsharp (generalized) measurement of with POVM given by and , for which we have , so that the POVM is an unsharp measurement of . Hence, we have , from . Appyling the definitions for error profile and locally uniform q-rms error of the unsharp measurement described by the POVM , one gets and , respectively. In the actual experiment the noisy POVM is realized by a randomized combination of a projective measurement of and a ‘no-measurement’. The probability , is measured by the projectors of , denoted as , i.e. , together with a contribution of a ‘no-measurement’. The ‘no-measurement’, (identity) is simply a measurement of spin operators, that are orthogonal to the plane spanned by the of the evolved states , namely for all , and therefore add up to identity. We can thus rewrite the POVM elements as , with as the weight for the ‘no-measurement’ and as weight of the projector. In the experiment this is achieved by controlling the current in DC coil 2 with a random generator, where with a frequency of 10 Hz either the current for the measurement or for one of the two orthogonal spin components of the ‘no-measurement’ is randomly chosen, which is plotted below in comparision with the projective measurement from before.

Now, in case of an unsharp measurement the last term of the sum of expectation values, given by is non-zero, since, . Acomparioson of the error profile and locally uniform q-rms error of the unsharp (generalized) and sharp (projective) measuremenr of M is given below.

1. S. Sponar, A. Danner, M. Ozawa, and Y. Hasegawa, npj Quantum Information 7, 106 (2021). ↩

2. M. Ozawa, npj Quantum Information 5, 1 (2019). ↩

3. P. Busch, T. Heinonen, and P. Lahti, Phys. Lett. A 320, 261–270 (2004). ↩