Twisting neutral particles with electric fields
January 10, 2024 2:12 pmIn our recent work 1 we demonstrate that spin-orbit entangled states are generated in neutral, non-zero magnetic moment, spin 1/2 particles, i.e., neutrons, travelling through an electric field. This interaction is relativistic in nature, arising from the relative motion between the neutron and an electric field. After all the only difference between an electric charge (source of electric field) and a current (source of magnetic field) is motion. Hence an observer moving through an electric field will experience a magnetic field in his rest frame. This magnetic field is given by , for . The neutron couples to this magnetic field via the Zeeman effect leading us to derive the Schwinger potential for low velocities , with the coupling constant. Spin-orbit states are generated when the electric field is polarized along the flight direction of the particles. You may be inclined to think that in this case the coupling is zero since , however due to the uncertainty principle it is impossible for the momentum to be perfectly parallel to the electric field. The uncertainty principle which when it comes to position and momentum really arises from Huygens principle will ensure that the beam always has a non zero divergence, which in turn leads to a non-zero Schwinger coupling. We can more easily see the spin-orbit entangling action if we assume (with neutron propagation in -direction) and transforming the potential to -space . So the Fourier transformed potential seen by a neutron in a static longitudinal electric field is identical to the potential of a magnetic quadrupole. The approximate real space solution of a neutron, initially in the zeroth OAM state, for such a potential is given by where the index refers to the spin state, denotes the beam divergence and denotes the initial amplitude of the respective spin state. Below we show an animation of a wavefunction traversing an electric field. One can see that the state is initially described by a pure zeroth order Bessel of first kind, which mixes and evolves into a first order Bessel over time as it traverses the medium. The OAM in this case is more likely to be intrinsic, since the effect of the Electric field is independent of the ratio between beam coherence and beam size (in contrast to the magnetic field methods).
We have discussed the distinction between intrinsic/extrinsic and longitudinal/transverse OAM and the various techniques used to generate these states. Finally we must look at methods for measuring neutron orbital angular momentum. In general there are a few ways to go about this. The simplest way is to measure the phase profile of the wave via interferometry as was done in the original neutron experiment 4. In the case of neutrons this method is ill-suited for intrinsic states, since the spatial resolution required excedes technical limitations at this time. Another consideration comes from the angular doppler shift. If a wave carrying OAM is measured in a rotating frames as opposed to an inertial frame the frequency will be shifted by , with the OAM of the wave and the angular velocity of the rotating frame. This angular Doppler shift can also be understood as the Sagnac effect 2. However this method requires significant time resolution and a measuring device capable of spinning fast enough. A final method, requiring entanglement, makes use of a mode converter which flips the sign of the OAM 3. Using this method we do not require spatial or temporal resolution. In optics this mode conversion is often accomplished by means of a dove prism. In the case of neutrons mode conversion is achieved by means of a triple reflection, which effectively rotates the plane perpendicular to the neutron propagation direction. For neutrons with transverse OAM we envision a polarized beam is passed through a spin-orbit entangler (i.e. an electric field), a mode converter and a disentangler. Finally the beam is spin analyzed. If the mode converter flips the OAM, the disentangler will fail thereby destroying the spin intereference, while if the converter does not flip the OAM the disentangler will restore the original state, thereby enabling interference. Hence by rotating the mode converter around the beam-axis we will see modulation appear at the detector. The setup is shown in a figure below.
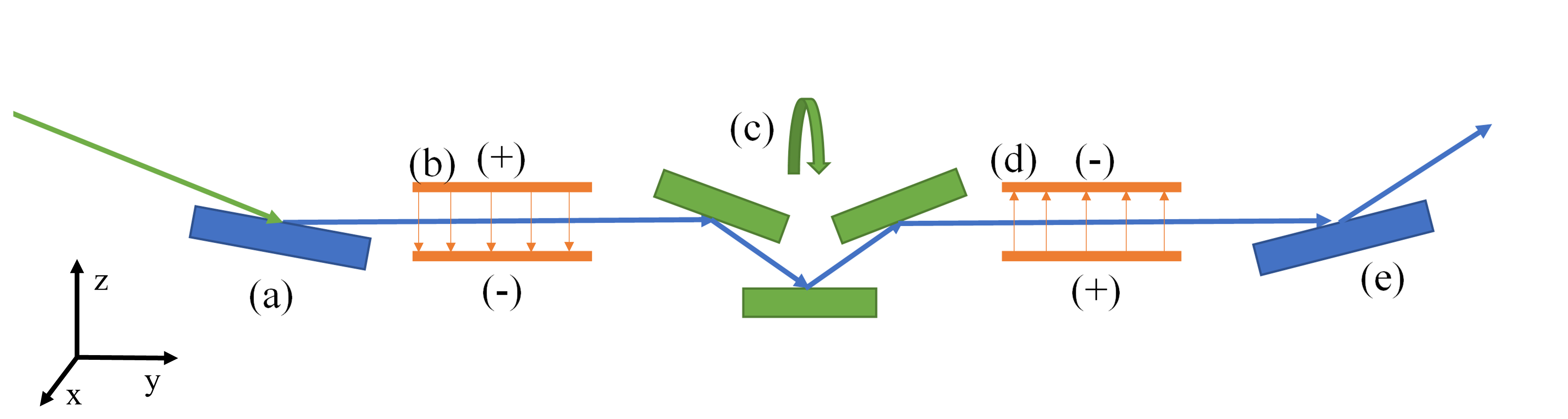
Schematic of the proposed concept experiment to demonstrate the generation of transverse OAM by electric fields. The setup consists of a polarizing supermirror (a), an electric beam twister (b), a set of non polarizing mirrors (mimicing a dove prism) which can be rotated around a common beam axis (c), another beam twister with opposite polarity (d) and a supermirror for spin polarization analysis (e).
References:
1. Niels Geerits and Stephan Sponar, Twisting Neutral Particles with Electric Fields, Phys. Rev. A 103, 022205 (2021). ↩
2. L. Allen, M. Babiker and W.L. Power, Azimuthal Doppler shift in light beams with orbital angular momentum, Optics Communications 112 (1994) 141-144. ↩
3. J. Leach, M.J. Padgett, S.M. Barnett, S. Franke-Arnold, and J. Courtial, Measuring the orbital angular momentum of a single photon, Physical Review Letters 88 (2002) 257901. ↩